Abstraction
A common concept you see often in multiple instances.
Numbers: 1,2,3,... 3400 BC, real numbers 760 BC


Generalization


- Weight/Distance/Time ⇒ Rational \(\frac{p}{q}\)
- Debts ⇒ Negative \(..., -2, -1, ? , 1, 2, ...\)
- Geometry ⇒ Irrational*
- Algebra ⇒ Complex
- \(0\) ⇒ "Nothing" become a number
& More things can be understood as numbers
& More operator to manipulate them.
Numbers ⇒ Sets
| Numbers | Set Theory (∞)/Abstract Algebra/Topology |
|---|---|
| \(\mathbb{N}\): \((+,0)\) | Semigroups |
| \(\mathbb{Z}\): \((+,0,\times,1)\) | Rings |
| \(\mathbb{Q}\) | Fields |
| \(\mathbb{R}\) | Complete Fields (topology) |
| \(\mathbb{C}\) | Algebræ |
| Modules,Vector Spaces, Monoids, ... |
& More general: more things are sets.
& More precise: clear distinction between concepts.
Sets ⇒? Categories
| Numbers | Sets | Categories |
|---|---|---|
| \(\mathbb{N}\): \((+,0)\) | Semigroups | ? |
| \(\mathbb{Z}\): \((+,0,\times,1)\) | Rings | ? |
| \(\mathbb{Q}\) | Fields | ? |
| \(\mathbb{R}\) | Complete Fields (topology) | ? |
| \(\mathbb{C}\) | Algebræ | ? |
| Modules,Vector Spaces, Monoids, ... | ? |
/.*/ ⇒? Category Theory
Gate between different scientific fields
- Topology
- Quantum Physics
- Logic
- Programming
& More general: more things are Categories.
& More precise: better distinction between concepts.
Young field: 1942–45, Samuel Eilenberg & Saunders Mac Lane
Programming & Abstraction
Impure programming
- Encouraged by imperative paradigms.
- Actions & mutable objects.
- Time is very important: ex. linked list push
- Synchronizing things is a challenge.
Natural Abstractions: pointers, variables, loop, Objects, Classes...
Representation: a data structure changing other time.
Untyped Pure Programming
- Time is irrelevant by default.
- Mostly static constructions like pipes.
- All pipes are round ⇒ all error at runtime
- (+ ("foo" 27) 32)
- Y = λf.(λx.f (x x)) (λx.f (x x))
- Y g = g (Y g)
Natural abstraction: higher level functions & equations
Strongly Typed Pure Programming
- Add specific forms on pipes.
-
4 + ["foo",27]forbidden -
["foo",27]forbidden
-
- Pipe can contains other pipes.
-
data Maybe a = Just a | Nothing -
[Just 32,Nothing,Just 12] :: [Maybe Integer]
-
Natural abstraction: Polymorphic higher level functions.
Polymorphism: mappend
(<>) = `mappend`
"abc" <> "def" = "abcdef"
("abc","xyz") <> ("ABC","XYZ") = ("abcABC","xyzXYZ")
3 <> 4 = ERROR which law? + or *
-- Monoid (N,+)
type Sum = Sum {getSum :: a}
(<>+) = getSum (Sum x <> Sum y)
3 <>+ 4 = 7
-- Monoid (N,*)
type Product = Product {getProduct :: a}
(<>*) = getProduct (Product x <> Product y)
3 <>* 4 = 12Polymorphism: (>>=)
Example: (>>=) with [a] and Maybe a
data Maybe a = Just a | Nothing-- Maybe : Maybe Int >>= Int -> Maybe (Int -> Int) >>= (Int -> Int) -> Maybe Int
(Just 2) >>= \x -> (Just (\z->z*z)) >>= \f -> Just (f x) = Just 4
Nothing >>= \x -> (Just (\z->z*z)) >>= \f -> Just (f x) = Nothing
-- Lists: [a] : [Int] >>= Int -> [Int -> Int] >>= (Int -> Int) -> [Int]
[1,2] >>= \x -> [(+10),(+20)] >>= \f -> [f x] = [11,21,12,22]
[] >>= \x -> [(+10),(+20)] >>= \f -> [f x] = []Programming Paradigms
| Impure | Choose the data structure, find an algorithm. |
| Untyped Pure | Choose the data structure, find an equation. |
| Typed Pure | Choose the Types and their laws, find the right operator |
Type Theory ⇒ Categories
- Type theory helped to remove paradoxes in Set Theory.
- Prevent relations between different kind of objects.
- Used in computer science
- typed λ-calculus ⇒ cartesian closed categories
- untyped λ-calculus ⇒ C-monoids (subclass of categories)
- Martin-Löf type theories ⇒ locally cartesian closed categories
Plan
- Why?
- What?
- Category
- Intuition
- Examples
- Functor
- Examples
- How?
Category
A way of representing things and ways to go between things.
A Category \(\mathcal{C}\) is defined by:
- Objects (\(\ob{C}\)),
- Morphisms (\(\hom{C}\)),
- a Composition law (∘)
- obeying some Properties.
Category: Objects
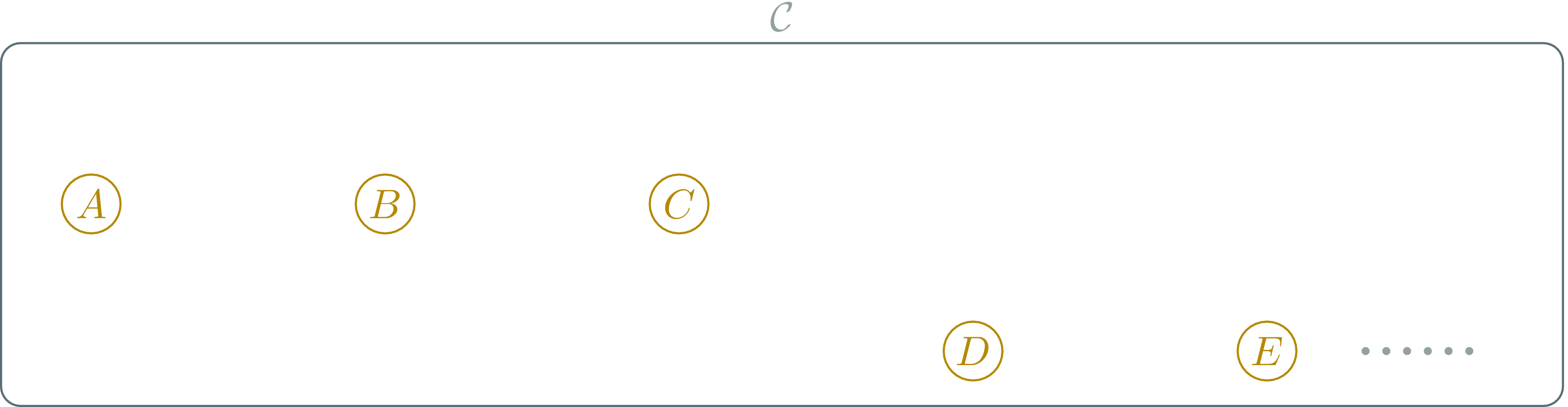
\(\ob{\mathcal{C}}\) is a collection
Category: Morphisms
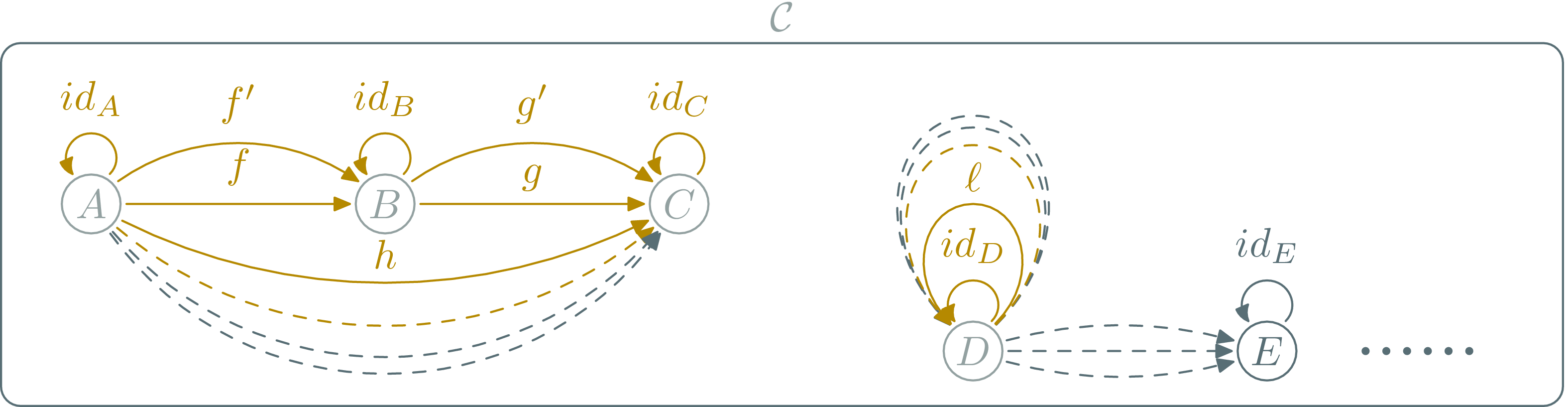
\(\hom{A,B}\) is a collection
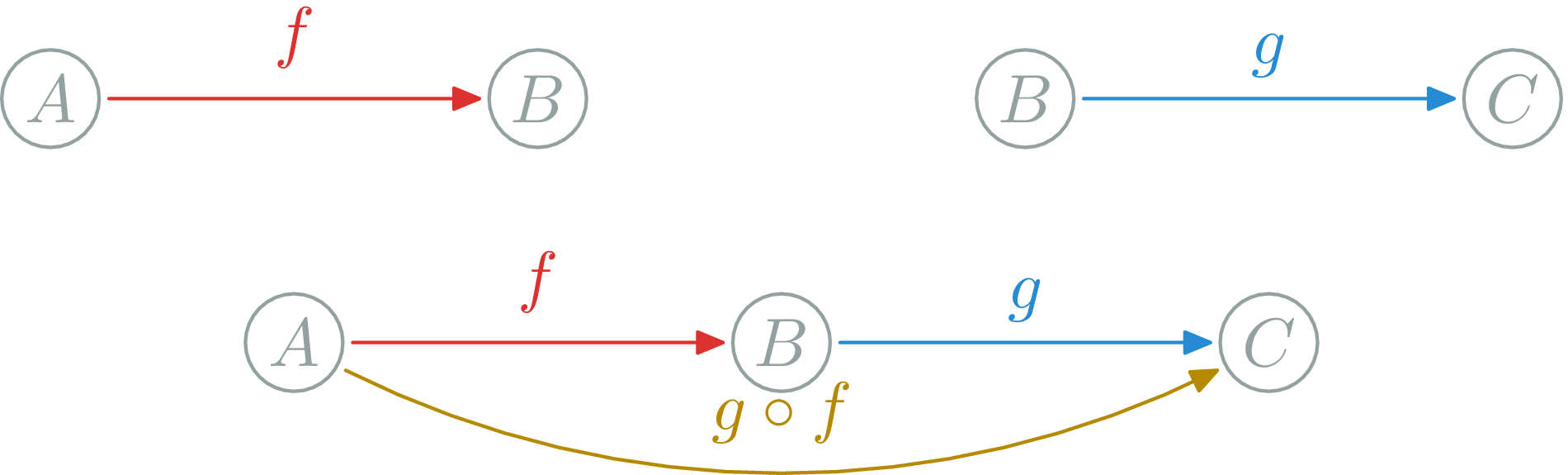
Category: Composition
Composition (∘): \(f:A→B, g:B→C\) $$g∘f:A\rightarrow C$$
Category laws: neutral element
for all \(X\), there is an \(\id_X\), s.t. for all \(f:A→B\):
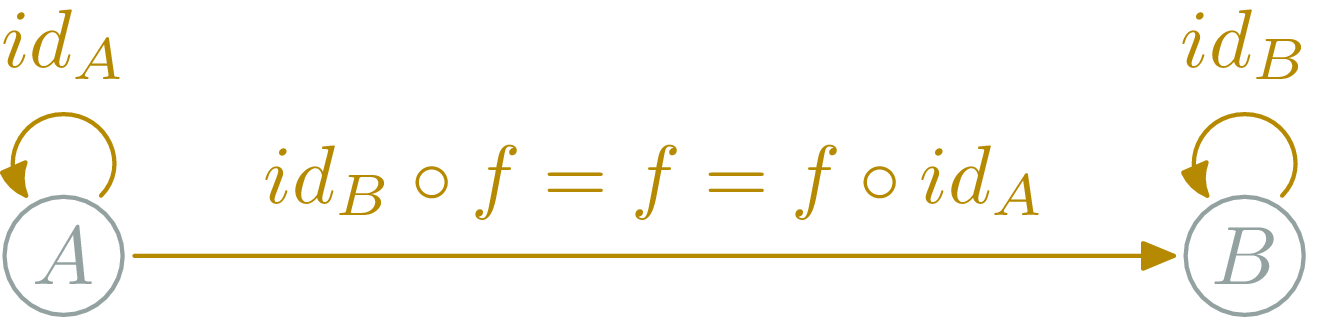
Category laws: Associativity
Composition is associative:
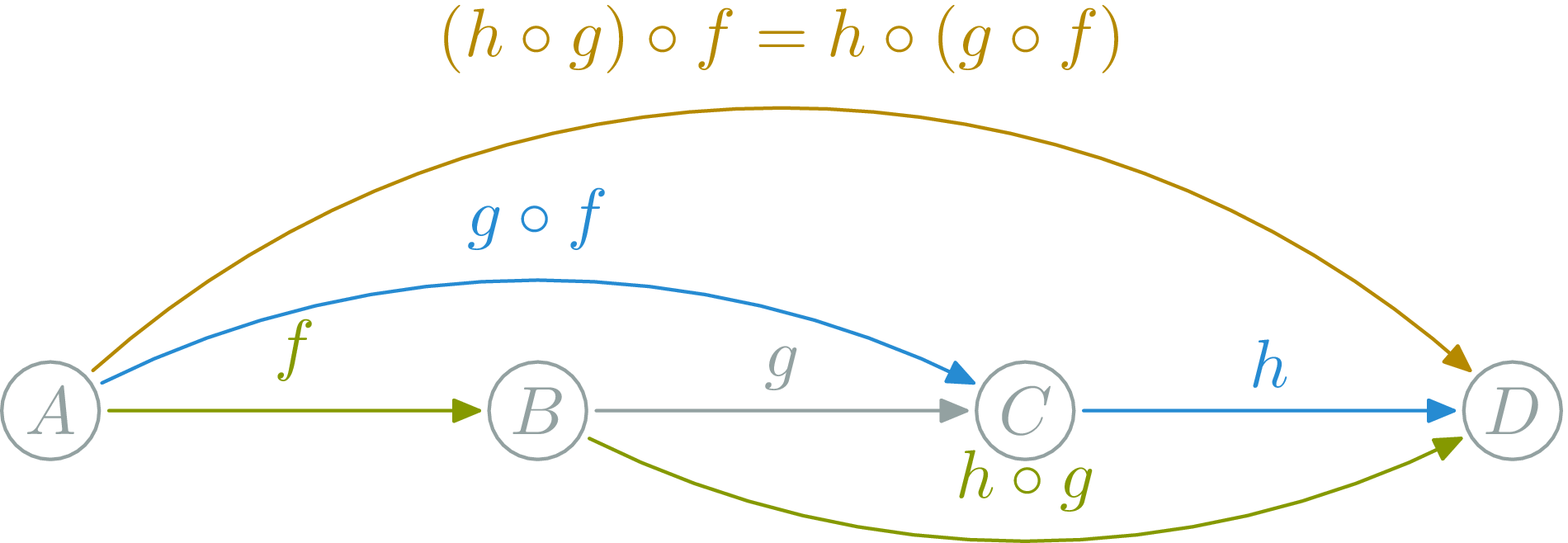
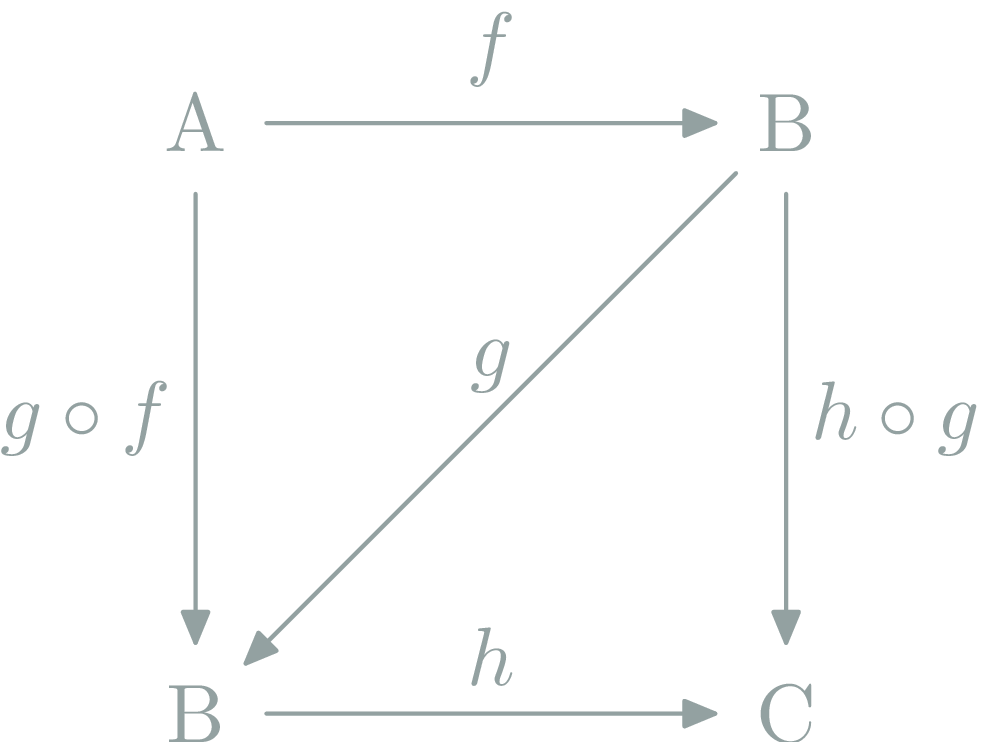
Commutative diagrams
Two path with the same source and destination are equal.
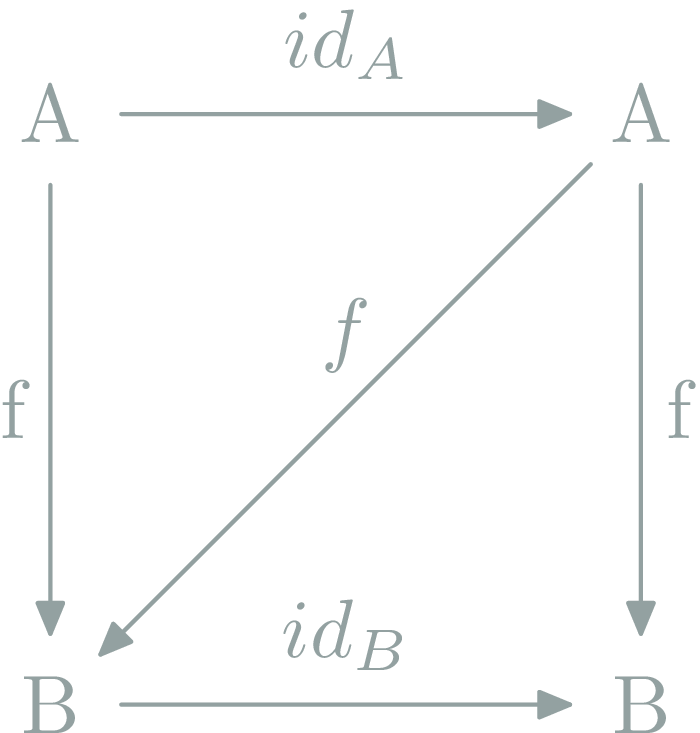
Can this be a category?


NO
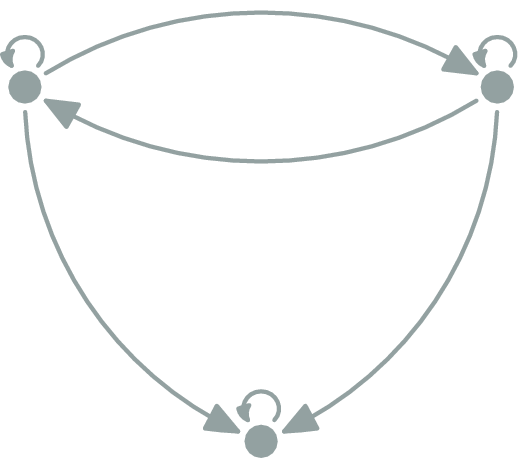
Can this be a category?
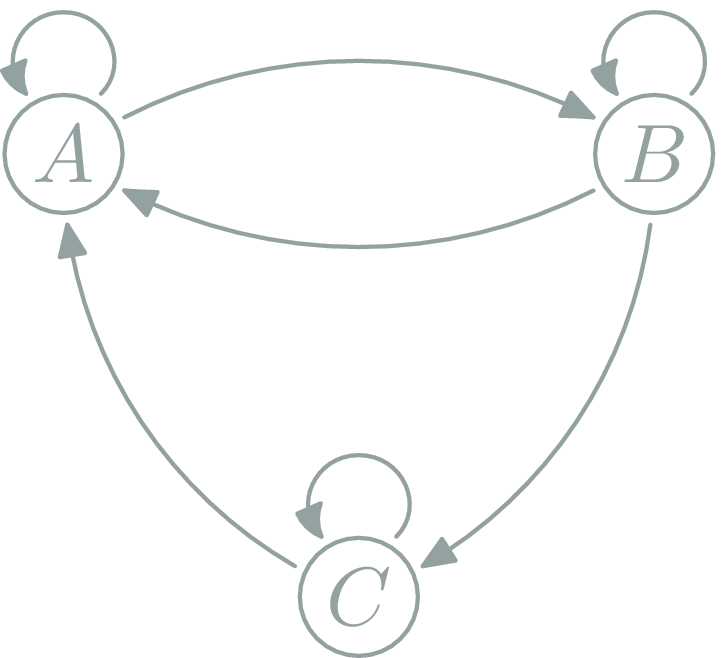
NO
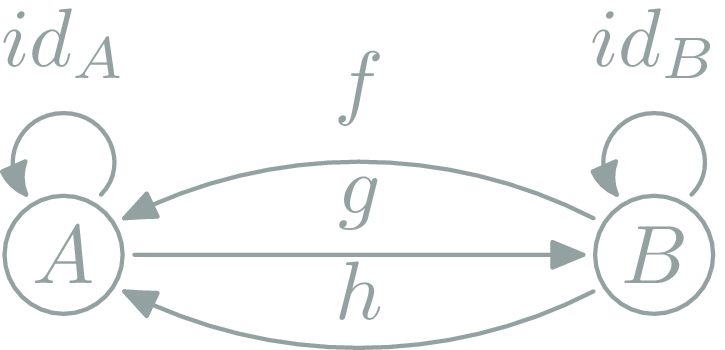
\(h∘(g∘f)=h∘\id_A=h\)
but \(h≠f\)
NO
Categories Everywhere?
\(\Set\)
- \(\ob{\Set}\) are sets
- \(\hom{\Set}\) are functions
- ∘ is functions composition
- \(\ob{\Set}\) is a proper class ; not a set
- \(\hom{E,F}\) is a set
- \(\Set\) is a locally small category
Categories Everywhere?
- \(\Mon\): (monoids, monoid morphisms,∘)
- \(\Vec\): (Vectorial spaces, linear functions,∘)
- \(\Grp\): (groups, group morphisms,∘)
- \(\Rng\): (rings, ring morphisms,∘)
- \( \ML\): (types, terms, \(λg. λf. λx. g f x\) )
- ...
Smaller Examples
Strings
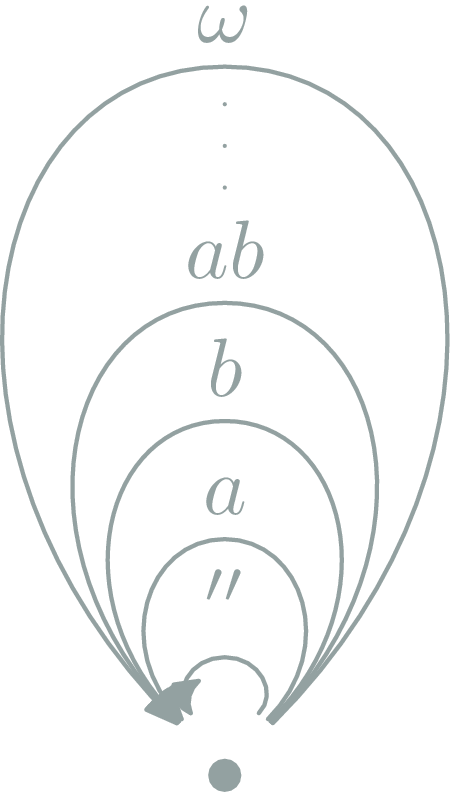
- \(\ob{Str}\) is a singleton
- \(\hom{Str}\) each string
- ∘ is concatenation
(++)
-
"" ++ u = u = u ++ "" -
(u ++ v) ++ w = u ++ (v ++ w)
Finite Example?
Graph

- \(\ob{G}={X,Y,Z}\),
- \(\hom{G}=\{ε,α,β,γ,αβ,βγ,...\}\)
\(\phantom{\hom{G}}=(βγ?)?(αβγ)^*(αβ?)?\), - \(αβ∘γ=αβγ\)
- \(\ob{G}\) are vertices
- \(\hom{G}\) each path
- ∘ is path concatenation
Degenerated Categories
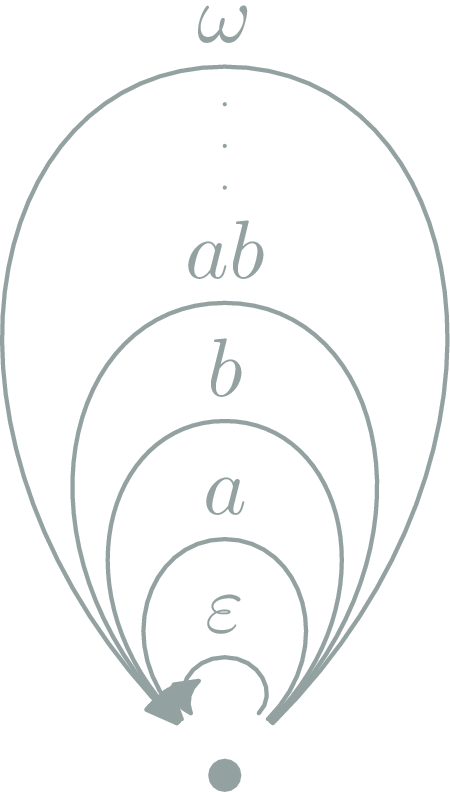
Monoids
each Monoid \((M,e,◎): \ob{M}=\{∙\},\hom{M}=M,\circ = ◎\)
one object
Examples: (Integer,0,+), (Integer,1,*), (Strings,"",++), (Lists,[],++), ...
Number construction
Each Numbers as a whole category
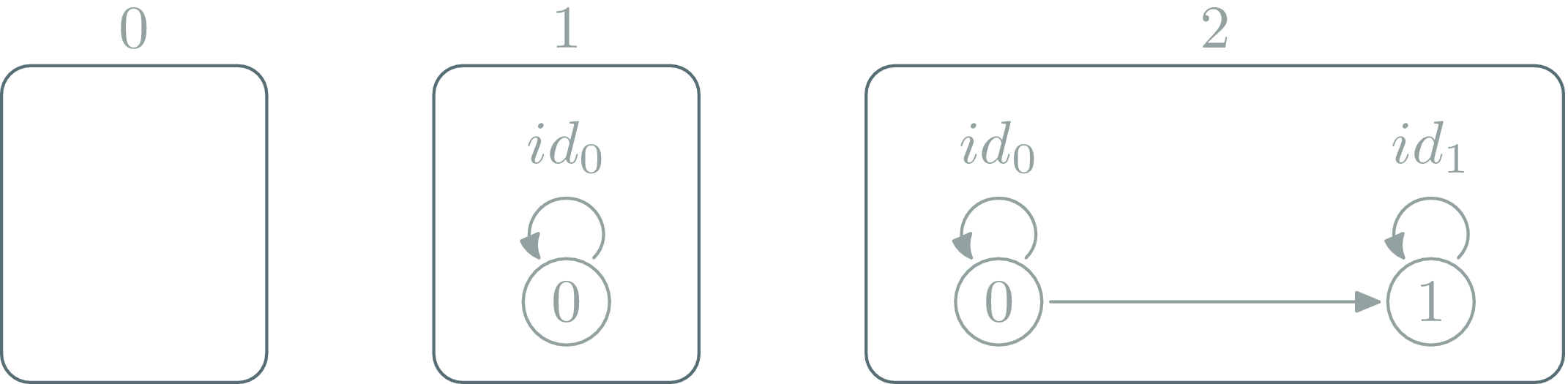
Degenerated Categories
Preorders
each preorder \((P,≤): \ob{P}={P},\hom{x,y}=\{{x≤y}\} ⇔ x≤y,f_{y,z} \circ f_{x,y} = f_{x,z} \)
At most one morphism between two objects.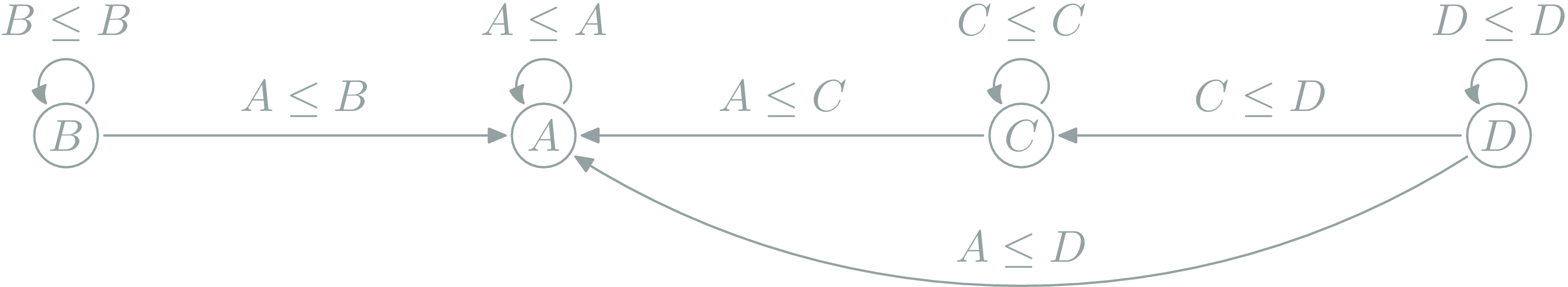
Degenerated Categories
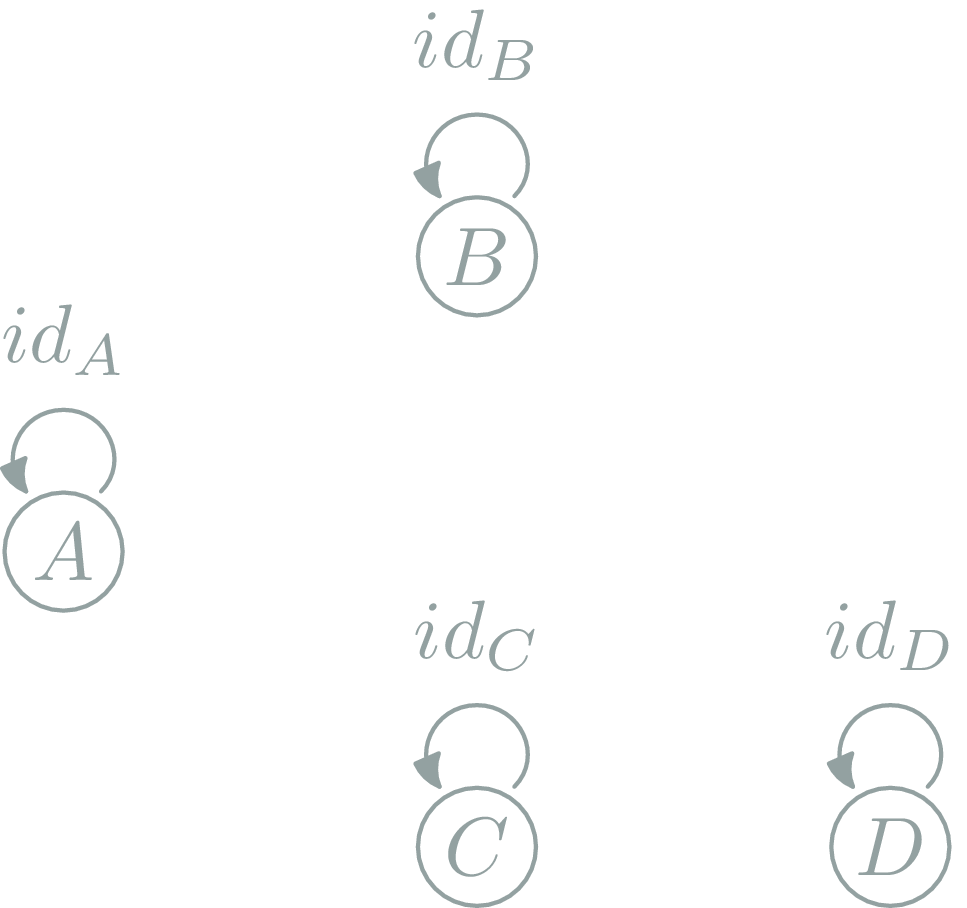
Any Set
Any set \(E: \ob{E}=E, \hom{x,y}=\{x\} ⇔ x=y \)
Only identities ; not so interesting
Functor
A functor is a mapping between two categories. Let \(\C\) and \(\D\) be two categories. A functor \(\F\) from \(\C\) to \(\D\):
- Associate objects: \(A\in\ob{\C}\) to \(\F(A) \in\ob{\D}\)
- Associate morphisms: \(f:A\to B\) to \(\F(f) : \F(A) \to \F(B)\)
such that
- \( \F (\id_X) = \id_{\F(X)} \),
- \( \F (g \circ_\C f) = \F(g) \circ_\D \F(f) \)
Functor Example (ob → ob)
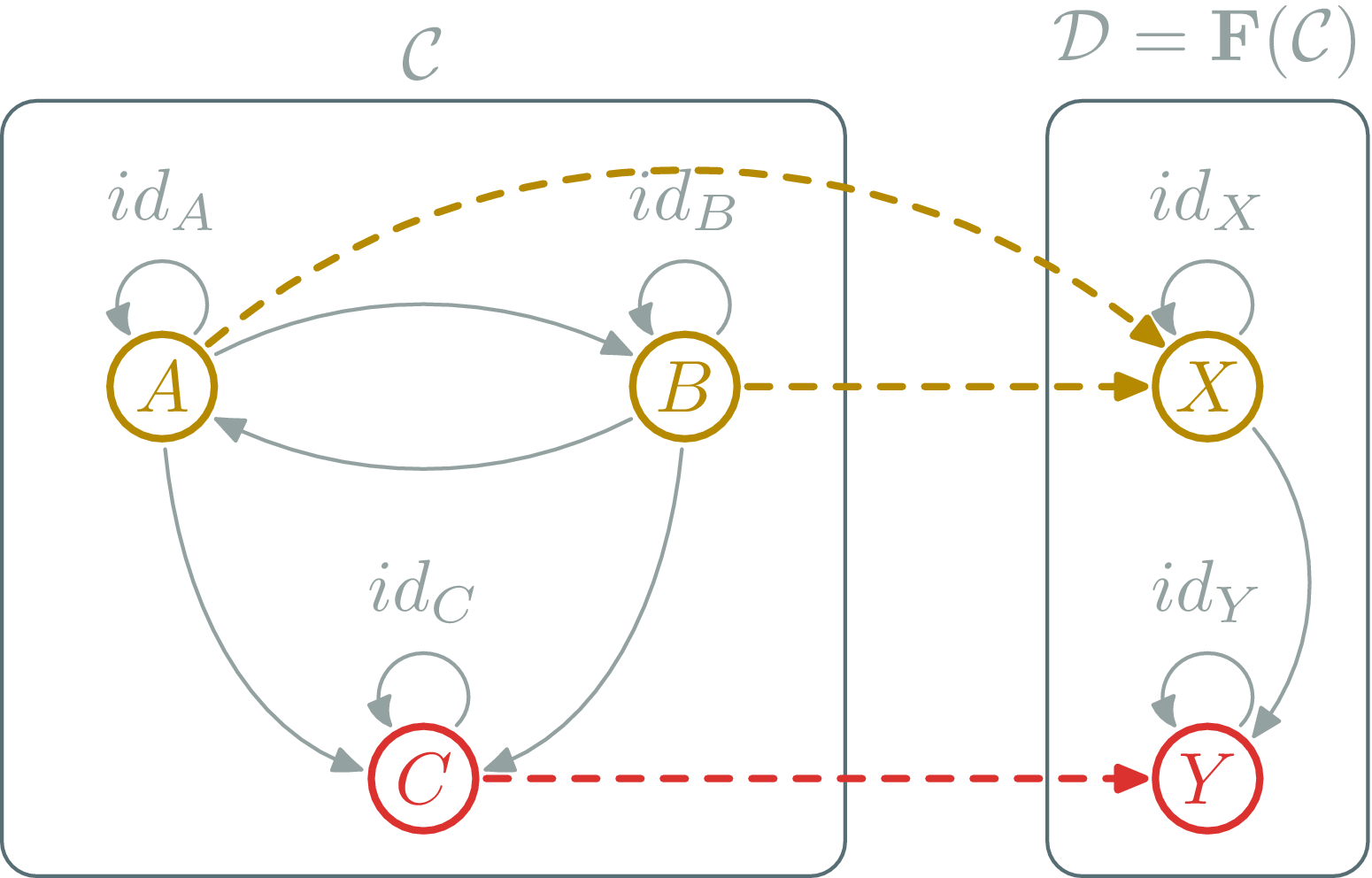
Functor Example (hom → hom)

Functor Example

Plan
- Why?
- What?
- How?
- \(\Hask\) category
- Functors
- Monads
- Arrows
- κατα-morphisms
Hask
Category \(\Hask\):
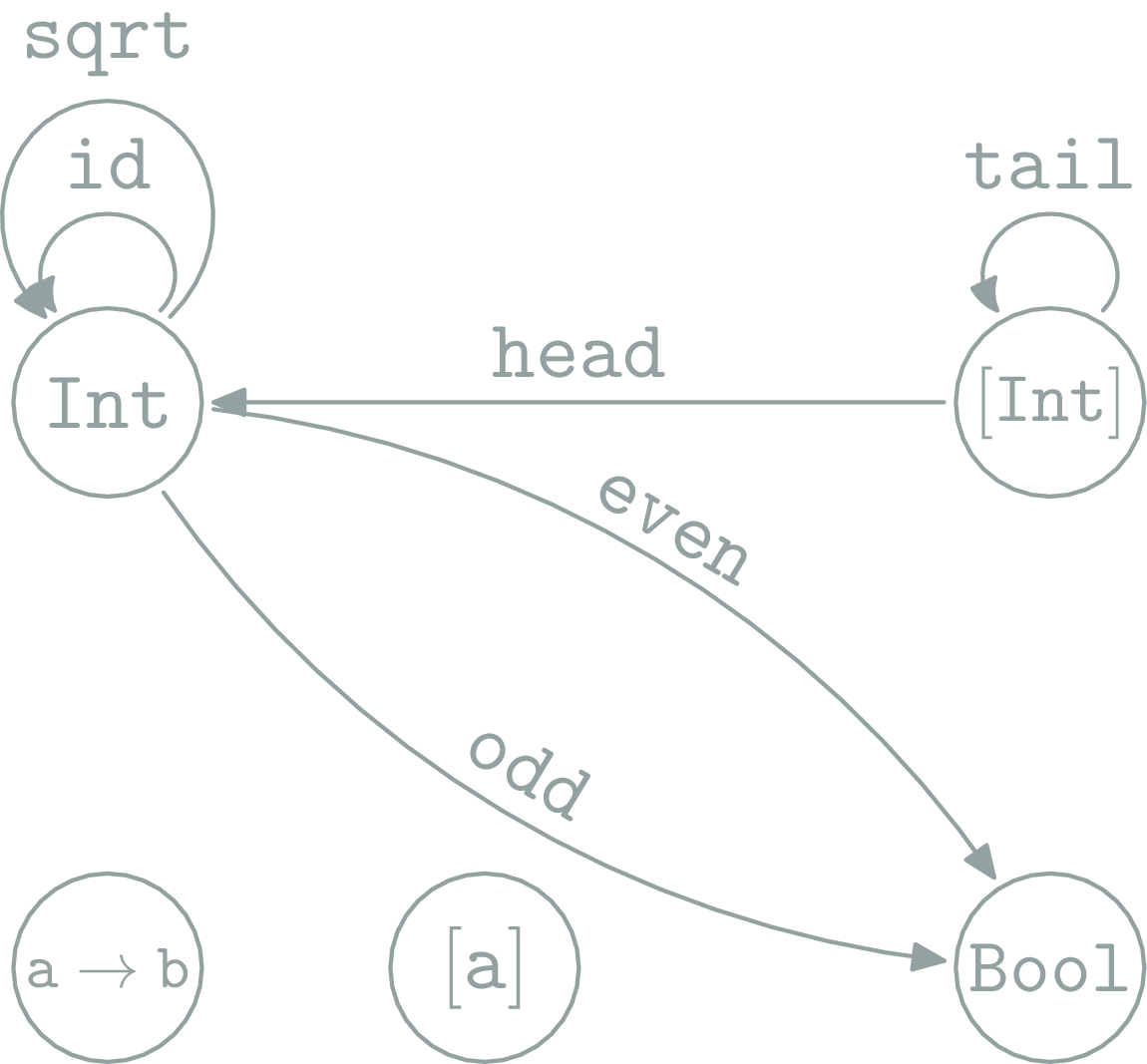
- \(ob(\Hask) = \) Haskell types
- \(hom(\Hask) = \) Haskell functions
-
∘ =
(.)Haskell function composition
Forget glitches because of undefined.
Haskell Functors
- Haskell Functors are from Hask to Hask; \(F:\C→\C\) are called endofunctors.
- Haskell Functors are Object of Hask.
- Notation:
- F <type> → <type> denoted
F :: * -> * - F <function> → <function>✗
fmap: <function> → <function>✓ choose F with polymorphism.
- F <type> → <type> denoted
- Properties
fmapmust obey for F to be a real functor:fmap id = idandfmap f.g = fmap f . fmap g
Haskell Functors Example: Maybe
data Maybe a = Just a | Nothing
instance Functor Maybe where
fmap :: (a -> b) -> (Maybe a -> Maybe b)
fmap f (Just a) = f a
fmap f Nothing = Nothing
fmap (+1) (Just 1) == 2
fmap (+1) Nothing == Nothing
fmap head (Just [1,2,3]) == Just 1
Haskell Functors Example: List
instance Functor ([]) where
fmap :: (a -> b) -> [a] -> [b]
fmap = map
fmap (+1) [1,2,3] == [2,3,4]
fmap (+1) [] == []
fmap head [[1,2,3],[4,5,6]] == [1,4]
String like type
data F a = Cons Char a | Nil
-- examples :
-- Cons 'c' 32 :: F Int
-- Cons 'c' (\x -> x*x) :: F (Int -> Int)
-- Cons 'c' (Cons 'a' (\x -> x*x)) :: F (F (Int -> Int))
-- Cons 'c' (Cons 'c' Nil) :: F (F (F))
-- note String is the fixed point of F: F(F(F(...)))
instance Functor F where
fmap :: (a -> b) -> [a] -> [b]
fmap f (Cons c x) = Cons c (f x)
fmap f Nil = Nil
fmap (+1) (Cons 'c' 3) == Cons 'c' 4
fmap (+1) Nil == Nil
fmap head (Cons 'c' [1,2,3])== Cons 'c' 1
Functor as boxes
Haskell functor can be seen as boxes containing all Haskell types and functions. Haskell types is fractal:
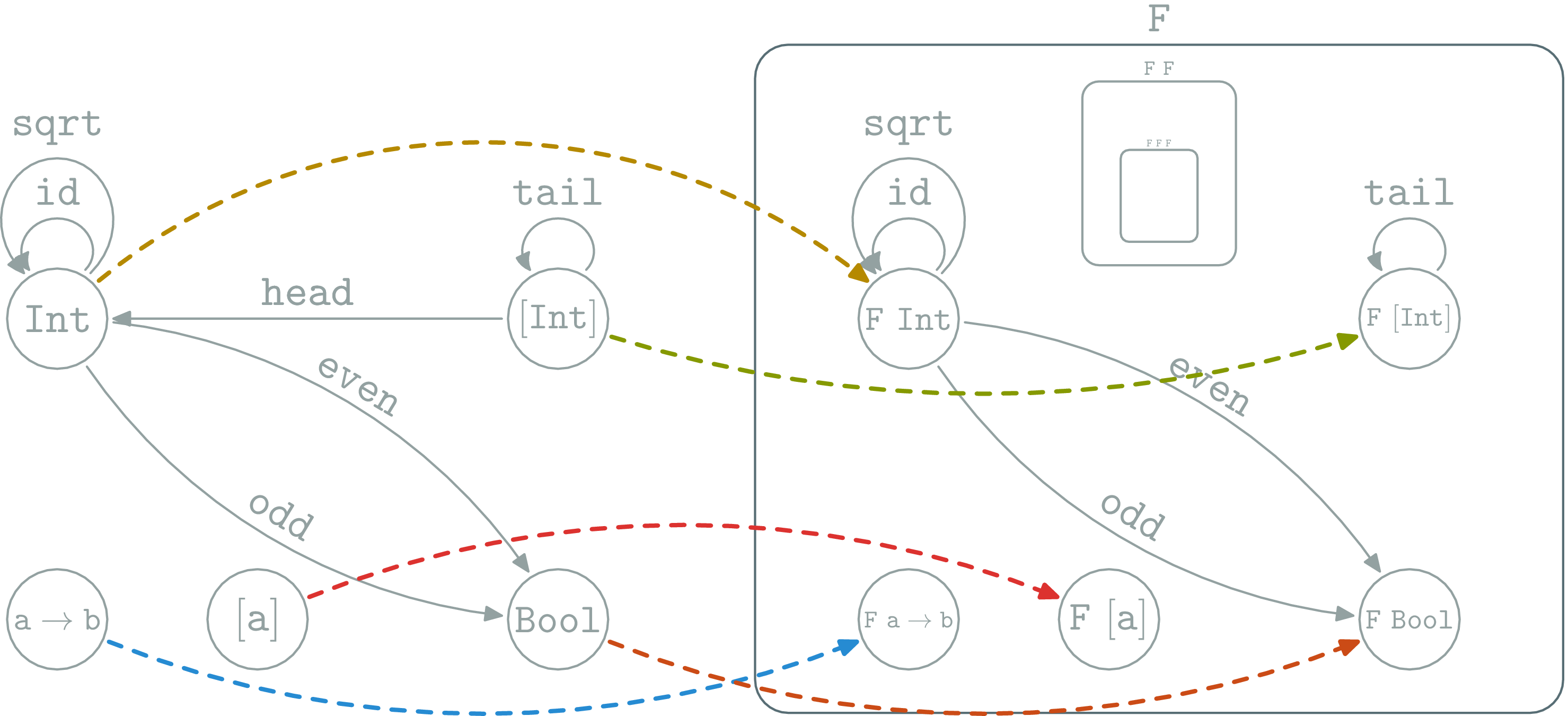
/
#